



Next: Discriminantes Lineares
Up: Extração de características
Previous: Transformada de Fourier
Sumário
PCA
Segundo Jain et al. [13], o melhor extrator de características linear conhecido é o de análise de componentes principais (PCA). Essa transformada é amplamente utilizada pela comunidade de reconhecimento de padrões e de reconhecimento de faces.
Conforme dito anteriormente, a transformada PCA, também conhecida por transformada de Hotelling e por expansão de Karhunen-Loève, é amplamente utilizada para efetuar reconhecimento de faces [38,24,2,26].
Visando tratar imagens como padrões em um espaço linear, sendo 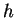 o número de linhas de uma imagem e
o número de linhas de uma imagem e 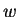 o número de colunas, pode-se dizer que uma imagem é um padrão de
o número de colunas, pode-se dizer que uma imagem é um padrão de 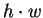 características, ou um vetor no espaço (
características, ou um vetor no espaço (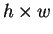 )-dimensional, o qual chamaremos de ``espaço de imagens''.
Dada uma imagem representada como uma matriz
)-dimensional, o qual chamaremos de ``espaço de imagens''.
Dada uma imagem representada como uma matriz 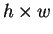 , pode-se construir sua representação como um vetor através de uma leitura linha a linha (raster) da imagem, colocando o valor de cada pixel da imagem em um vetor coluna, o qual é inserido na matriz
, pode-se construir sua representação como um vetor através de uma leitura linha a linha (raster) da imagem, colocando o valor de cada pixel da imagem em um vetor coluna, o qual é inserido na matriz 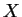 . Ou seja, dada uma matriz
. Ou seja, dada uma matriz 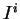 de
de 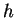 linhas e
linhas e 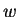 colunas representando a imagem
colunas representando a imagem 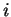 ,
,
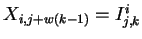 , para
, para
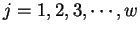 ,
,
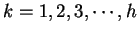 e
e
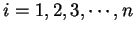 , em que
, em que 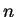 é o tamanho do conjunto de treinamento e
é o tamanho do conjunto de treinamento e 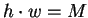 (vide equação 1).
Em reconhecimento de padrões, é sempre desejável dispor de uma representação compacta e com um bom poder de discriminação de classes de padrões. Para isso, é desejável que não haja redundância entre as diferentes características dos padrões, ou seja, que não haja covariância entre as bases do espaço de características. Mas, obviamente, pode-se notar que o espaço de imagens é altamente redundante quando usado para descrever faces, pois cada pixel é altamente correlacionado com outros pixels.
Para verificar se há covariância entre as características (ou variáveis), utiliza-se a matriz de covariância dos padrões [46,14]. Dada uma matriz de padrões
(vide equação 1).
Em reconhecimento de padrões, é sempre desejável dispor de uma representação compacta e com um bom poder de discriminação de classes de padrões. Para isso, é desejável que não haja redundância entre as diferentes características dos padrões, ou seja, que não haja covariância entre as bases do espaço de características. Mas, obviamente, pode-se notar que o espaço de imagens é altamente redundante quando usado para descrever faces, pois cada pixel é altamente correlacionado com outros pixels.
Para verificar se há covariância entre as características (ou variáveis), utiliza-se a matriz de covariância dos padrões [46,14]. Dada uma matriz de padrões 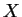 conforme definida na equação 1, a matriz
conforme definida na equação 1, a matriz 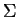 de covariância de
de covariância de 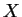 pode ser obtida por:
pode ser obtida por:
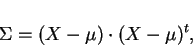 |
(6) |
em que 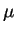 é a matriz
é a matriz 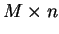 (mesma dimensão que
(mesma dimensão que 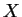 ), em que todas suas colunas contém o valor esperado de
), em que todas suas colunas contém o valor esperado de 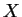 , o qual pode ser obtido pela média aritmética das colunas de
, o qual pode ser obtido pela média aritmética das colunas de 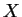 . Ou seja:
. Ou seja:
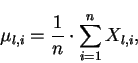 |
(7) |
para
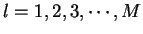 .
É importante notar que
.
É importante notar que 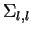 é a variância da característica
é a variância da característica 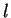 dos padrões (
dos padrões (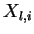 , para todo
, para todo
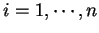 ). Ou seja, os elementos da diagonal da matriz de covariância se referem à variância das características. Já os elementos fora da diagonal
). Ou seja, os elementos da diagonal da matriz de covariância se referem à variância das características. Já os elementos fora da diagonal 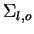 representam a covariância entre a característica
representam a covariância entre a característica 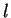 e
e 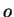 . Se duas características,
. Se duas características, 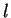 e
e 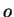 , são estatisticamente independentes, a covariância é nula (
, são estatisticamente independentes, a covariância é nula (
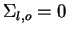 ).
Conforme dito anteriormente, é desejável que os padrões sejam representados em um espaço em que não haja covariância entre características diferentes. Um espaço vetorial com essa propriedade possui uma base cuja matriz de covariância de seus vetores é diagonal. Partindo-se de um conjunto de exemplos de padrões de treinamento, para obter uma base com tal propriedade basta utilizar uma transformada que diagonalize a matriz de covariância da base atual do espaço. Com a diagonalização da matriz de covariância, a variância das variáveis (características) será maximizada e a covariância entre uma variável e outra será nula.
Devido ao processo de criação da matriz de covariância, pode-se mostrar que ela é diagonalizável [12,14,47]. A diagonalização é realizada através dos auto-vetores de
).
Conforme dito anteriormente, é desejável que os padrões sejam representados em um espaço em que não haja covariância entre características diferentes. Um espaço vetorial com essa propriedade possui uma base cuja matriz de covariância de seus vetores é diagonal. Partindo-se de um conjunto de exemplos de padrões de treinamento, para obter uma base com tal propriedade basta utilizar uma transformada que diagonalize a matriz de covariância da base atual do espaço. Com a diagonalização da matriz de covariância, a variância das variáveis (características) será maximizada e a covariância entre uma variável e outra será nula.
Devido ao processo de criação da matriz de covariância, pode-se mostrar que ela é diagonalizável [12,14,47]. A diagonalização é realizada através dos auto-vetores de 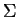 [47], ou seja, a matriz
[47], ou seja, a matriz 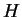
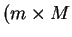 ) da equação 1 deve ser obtida através dos auto-vetores da matriz
) da equação 1 deve ser obtida através dos auto-vetores da matriz 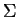 dispostos cada um em uma linha. Maiores detalhes a respeito de obtenção de auto-valores e auto-vetores podem ser encontrados em [47].
É importante lembrar que os auto-valores refletem a importância dos auto-vetores. No caso de PCA, os auto-valores da matriz de covariância são iguais à variância das características transformadas [12]. Assim, se um auto-vetor possui auto-valor grande, significa que este fica em uma direção em que há uma grande variância dos padrões. A importância desse fato está na classificação, pois, em geral, é mais fácil distinguir padrões usando uma base em que seus vetores não são correlacionados e que apontam para a direção da maior variância dos dados.
Através das figuras 3, 4 e 5 pode-se visualizar o efeito da transformada PCA para o caso bidimensional. Pode-se notar que é realizada uma rotação da base do espaço vetorial de forma que o primeiro vetor da nova base fique na direção em que há maior variância dos dados e o segundo fique perpendicular ao primeiro, na direção da segunda maior variação.
dispostos cada um em uma linha. Maiores detalhes a respeito de obtenção de auto-valores e auto-vetores podem ser encontrados em [47].
É importante lembrar que os auto-valores refletem a importância dos auto-vetores. No caso de PCA, os auto-valores da matriz de covariância são iguais à variância das características transformadas [12]. Assim, se um auto-vetor possui auto-valor grande, significa que este fica em uma direção em que há uma grande variância dos padrões. A importância desse fato está na classificação, pois, em geral, é mais fácil distinguir padrões usando uma base em que seus vetores não são correlacionados e que apontam para a direção da maior variância dos dados.
Através das figuras 3, 4 e 5 pode-se visualizar o efeito da transformada PCA para o caso bidimensional. Pode-se notar que é realizada uma rotação da base do espaço vetorial de forma que o primeiro vetor da nova base fique na direção em que há maior variância dos dados e o segundo fique perpendicular ao primeiro, na direção da segunda maior variação.
Figura 3:
Dados artificiais bidimensionais.
|
|
Figura:
Dados de teste com os auto-vetores da matriz de covariância e seus respectivos auto-valores.
|
|
Figura:
Dados no espaço criado.
|
|
O número de auto-vetores obtido é, no máximo, igual ao número de pixels da imagem (ou variáveis dos padrões de entrada). Porém, conforme dito acima, se a matriz 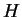 for construída de forma que forem escolhidos somente os auto-vetores contendo os maiores auto-valores, a variância total dos padrões de entrada não sofre grandes mudanças. Assim, é possível realizar redução de dimensionalidade utilizando-se, na construção de
for construída de forma que forem escolhidos somente os auto-vetores contendo os maiores auto-valores, a variância total dos padrões de entrada não sofre grandes mudanças. Assim, é possível realizar redução de dimensionalidade utilizando-se, na construção de 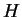 , somente os
, somente os 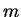 maiores auto-vetores, de forma que a dimensionalidade de
maiores auto-vetores, de forma que a dimensionalidade de 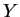 será
será 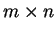 , o que significa uma redução de dimensionalidade de
, o que significa uma redução de dimensionalidade de 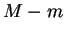 dimensões. Após a redução da dimensionalidade com PCA, em geral, para reconhecimento de faces, a classificação é efetuada utilizando-se o classificador do vizinho mais próximo (vide seção 6).
A transformada PCA é relativamente simples, mas o processo de treinamento é complexo, visto que, dentre outras operações, é necessário efetuar
dimensões. Após a redução da dimensionalidade com PCA, em geral, para reconhecimento de faces, a classificação é efetuada utilizando-se o classificador do vizinho mais próximo (vide seção 6).
A transformada PCA é relativamente simples, mas o processo de treinamento é complexo, visto que, dentre outras operações, é necessário efetuar
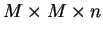 multiplicações para criar a matriz de covariância
multiplicações para criar a matriz de covariância 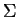 [18]. Porém a aplicação é muito rápida e, em geral, produz bons resultados para reconhecimento de faces. Mas segundo [14], PCA é uma técnica de extração de características não supervisionada propícia para dados com distribuição Gaussiana, mas não se tem certeza de que as faces possuam tal distribuição. Através das figuras 6, 7 e 8 pode-se observar um caso simples bidimensional em que, caso seja feita uma redução de dimensionalidade, será muito mais difícil distinguir os dois padrões, pois o segundo auto-vetor é melhor para distinguir as duas classes do que o primeiro.
[18]. Porém a aplicação é muito rápida e, em geral, produz bons resultados para reconhecimento de faces. Mas segundo [14], PCA é uma técnica de extração de características não supervisionada propícia para dados com distribuição Gaussiana, mas não se tem certeza de que as faces possuam tal distribuição. Através das figuras 6, 7 e 8 pode-se observar um caso simples bidimensional em que, caso seja feita uma redução de dimensionalidade, será muito mais difícil distinguir os dois padrões, pois o segundo auto-vetor é melhor para distinguir as duas classes do que o primeiro.
Figura:
Dados artificiais de teste: duas classes em um espaço bidimensional.
|
|
Figura:
Dados de teste de duas classes com os auto-vetores da matriz de covariância e seus respectivos auto-valores.
|
|
Figura:
Dados no espaço criado: note que o primeiro auto-vetor não possui poder de discriminação.
|
|
Conforme será descrito posteriormente, uma forma de eliminar esse problema consiste na aplicação de um algoritmo de seleção de características (vide seção 5).




Next: Discriminantes Lineares
Up: Extração de características
Previous: Transformada de Fourier
Sumário
Teofilo Emidio de Campos
2000-09-18
![\includegraphics[width=5cm, height=8cm]{pca_vet1.eps}](img51.png)
![\includegraphics[width=5cm, height=8cm]{pca_vet.eps}](img56.png)