



Next: Métodos estocásticos com múltiplas
Up: Algoritmos de seleção
Previous: Redes Neurais
Sumário
Em termos de resultado obtido, o único método realmente ótimo é o da busca exaustiva, que avalia todos os 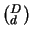 subconjuntos possíveis de tamanho
subconjuntos possíveis de tamanho 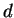 . Essa abordagem é muito cara computacionalmente mesmo para conjuntos não muito grandes, pois sua complexidade é exponencial.
Algumas funções critério possuem uma propriedade chamada monotonicidade. Uma função é monotônica se
. Essa abordagem é muito cara computacionalmente mesmo para conjuntos não muito grandes, pois sua complexidade é exponencial.
Algumas funções critério possuem uma propriedade chamada monotonicidade. Uma função é monotônica se
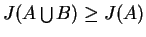 , para todo
, para todo
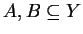 , ou seja, o valor da função critério é sempre maior para conjuntos de características maiores. Para este caso, há o algoritmo de busca em árvores chamado branch-and-bound [50]. Esse algoritmo pode retornar a solução ideal sem verificar todas as possibilidades, mas sabemos que, devido a curse of dimensionality (vide seção 3.1), para situações em que o conjunto de treinamento não é grande o suficiente, a função critério não é monotônica. Por esse fato, o algoritmo branch-and-bound não pode ser aplicado em qualquer situação.
Outra desvantagem desse método é que, no pior caso, todas as configurações são consultadas, o que faz com que o algoritmo tenha complexidade exponencial no pior caso, o que o torna impraticável para grandes conjuntos de características.
, ou seja, o valor da função critério é sempre maior para conjuntos de características maiores. Para este caso, há o algoritmo de busca em árvores chamado branch-and-bound [50]. Esse algoritmo pode retornar a solução ideal sem verificar todas as possibilidades, mas sabemos que, devido a curse of dimensionality (vide seção 3.1), para situações em que o conjunto de treinamento não é grande o suficiente, a função critério não é monotônica. Por esse fato, o algoritmo branch-and-bound não pode ser aplicado em qualquer situação.
Outra desvantagem desse método é que, no pior caso, todas as configurações são consultadas, o que faz com que o algoritmo tenha complexidade exponencial no pior caso, o que o torna impraticável para grandes conjuntos de características.
Teofilo Emidio de Campos
2000-09-18