são operadores binários (necessitam de dois operandos, ou seja, dois valores para operar). Eles são usados para combinar condições simples (ex: saída de operadores relacionais) ou o resultado de outros operadores lógicos, de modo a criar operações lógicas mais complexas.
O operador not ('não/negação' em português) é um operador unário. Seu resultado é sempre o inverso (a negação) do operando.
Sejam exp1 e exp2 expressões resultando em valores booleanos (True ou False), temos então:

As tabelas abaixo mostram os resultados dos três operadores lógicos Python para todas possíveis
combinações de seus valores de entrada.
Tabela verdade dos operadores and e or:
A | B | A and B | A or B |
|---|
False | False | False | False |
False | True | False | True |
True | False | False | True |
True | True | True | True |
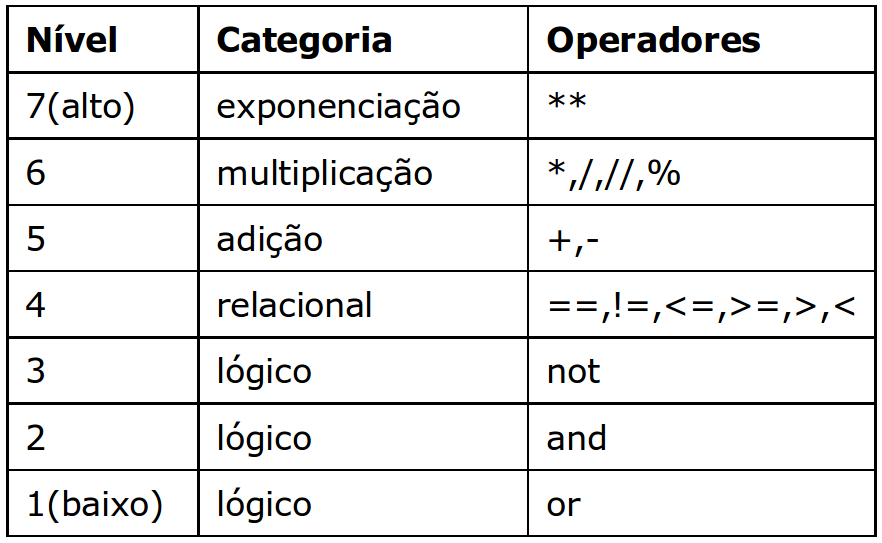
A tabela abaixo mostra a precedência dos operadores em Python. Isto significa que, em uma expressão, Python avaliará primeiro os operadores de maior nível.
Uma aplicação dos operadores lógicos
consiste na simplificação da escrita de comandos condicionais.
Veja as seguintes equivalências.
Equivalências:


Exemplo:
Encontrar a variável de maior valor entre três variáveis inteiras a, b e c com valores distintos.
Solução 1: Sem o uso de operadores lógicos
if a > b:
if a > c:
print("a é o maior")
else:
print("c é o maior")
else:
if b > c:
print("b é o maior")
else:
print("c é o maior")
Solução 2: Solução mais compacta com o uso de operadores lógicos
if a > b and a > c :
print("a é o maior")
elif b > c :
print("b é o maior")
else:
print("c é o maior")
Na álgebra booleana são válidas as seguintes propriedades/identidades:
| Propriedades Comutativas | A and B = B and A | A or B = B or A |
|---|
| Propriedades Distributivas | A and (B or C) = (A and B) or (A and C) | A or (B and C) = (A or B) and (A or C) |
|---|
| Propriedades Associativas | (A or B) or C = A or (B or C) | (A and B) and C = A and (B and C) |
|---|
| Propriedades Idempotentes | A and A = A | A or A = A |
|---|
| Dupla Negação | not not A = A |
|---|
| Elementos Absorventes | A or True = True | A and False = False |
|---|
| Elementos Neutros | A or False = A | A and True = A |
|---|
| Leis de De Morgan | not (A or B) = (not A) and (not B) | not (A and B) = (not A) or (not B) |
|---|
Abaixo é apresentado um exemplo de manipulação de uma expressão, usando as propriedades acima listadas, de modo a trocar um operador or por um operador and.
Considere a expressão:
(x < 3) or (y == 0)
Podemos aplicar a dupla negação sem alterar seu resultado:
not not ((x < 3) or (y == 0))
Podemos agora trocar o operador or pelo operador and, aplicando a "Leis de De Morgan":
not (not (x < 3) and not (y == 0))
Finalmente, podemos então simplificar a expressão, trocando os operadores relacionais negados por operadores relacionais complementares:
not (x >= 3 and y != 0)
Curiosidades:
Em linguagem C, o operador lógico
and se escreve como
&&
e o operador lógico
or como
||.
Em linguagem C, os valores booleanos False e True
são definidos como os valores numéricos 0 e 1, respectivamente.
Isso significa que o mesmo efeito do operador lógico and pode
ser obtido em C através de um simples produto, isto é, A && B
pode ser obtido como A * B. Porém, observe que a multiplicação
possui maior nível de precedência, o que pode gerar alterações na ordem de
execução no caso de expressões mais complexas, consequentemente levando a um resultado
diferente do esperado.
Já no caso do operador lógico or temos que
A || B pode ter o seu efeito reproduzido pela expressão A+B-A*B.
No Python 3, o tipo bool de dados booleanos é uma subclasse dos inteiros.
Logo, no Python 3, os valores booleanos False e True se comportam como os valores 0 e 1, respectivamente, em quase todos os contextos, a exceção é que, quando convertidos em uma string, as strings "False" ou "True" são retornadas, respectivamente.
Experimente digitar no prompt (>>>) do Python shell os comandos abaixo:
>>> 1 == True
True
>>> 0 == True
False
>>> 0 == False
True
>>> 1 == False
False
>>> str(1)
'1'
>>> str(True)
'True'
>>> str(0)
'0'
>>> str(False)
'False'
Problema 1:
Escreva um programa que determina a data
cronologicamente maior entre duas datas fornecidas
pelo usuário. Cada data deve ser fornecida por
três valores inteiros onde o primeiro representa
um dia, o segundo um mês e o terceiro um ano.
Solução 1: Sem o uso de operadores lógicos
# Primeira data.
d1 = int(input("Dia: "))
m1 = int(input("Mês: "))
a1 = int(input("Ano: "))
# Segunda data.
d2 = int(input("Dia: "))
m2 = int(input("Mês: "))
a2 = int(input("Ano: "))
if a1 > a2:
print("Data1 é maior!")
elif a1 == a2:
if m1 > m2:
print("Data1 é maior!")
elif m1 == m2:
if d1 > d2:
print("Data1 é maior!")
elif d1 == d2:
print("Datas são iguais!")
else:
print("Data2 é maior!")
else:
print("Data2 é maior!")
else:
print("Data2 é maior!")
Solução 2: Solução mais compacta com o uso de operadores lógicos
# Primeira data.
d1 = int(input("Dia: "))
m1 = int(input("Mês: "))
a1 = int(input("Ano: "))
# Segunda data.
d2 = int(input("Dia: "))
m2 = int(input("Mês: "))
a2 = int(input("Ano: "))
if a1>a2 or (a1==a2 and m1>m2) or (a1==a2 and m1==m2 and d1>d2):
print("Data1 é maior!")
elif a1==a2 and m1==m2 and d1==d2:
print("Datas são iguais!")
else:
print("Data2 é maior!")
Solução 3:
Segundo a propriedade distributiva
da álgebra booleana temos:
expr1 and (expr2 or expr3) = (expr1 and expr2) or (expr1 and expr3)
Logo, uma outra solução pode ser obtida colocando a condição
a1==a2 em evidência:
# Primeira data.
d1 = int(input("Dia: "))
m1 = int(input("Mês: "))
a1 = int(input("Ano: "))
# Segunda data.
d2 = int(input("Dia: "))
m2 = int(input("Mês: "))
a2 = int(input("Ano: "))
if a1>a2 or (a1==a2 and (m1>m2 or (m1==m2 and d1>d2))):
print("Data1 é maior!")
elif a1==a2 and m1==m2 and d1==d2:
print("Datas são iguais!")
else:
print("Data2 é maior!")
Problema 2:
Dados um número inteiro n>0 e as
notas de n alunos, determinar quantos
ficaram de recuperação. Um aluno está
de recuperação se sua
nota final for maior ou igual a 3 e menor do que 5.
Solução 1:
Uma solução usando operadores lógicos:
n = int(input("Digite n: "))
rec = 0
i = 1
while i <= n:
nota = float(input("Digite uma nota: "))
if 3.0 <= nota and nota < 5.0:
rec = rec + 1
i = i + 1
print(rec,"alunos ficaram de recuperação")
Do ponto de vista gráfico, usando a notação de conjuntos de intervalos na reta dos reais, temos:
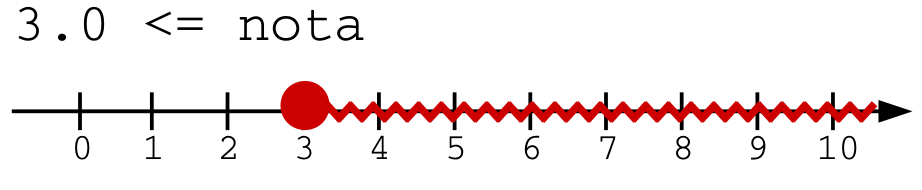


Observe que graficamente o operador lógico "and"
possui o efeito de intersecção dos conjuntos.
Solução 2:
Uma segunda solução sem usar operadores lógicos:
n = int(input("Digite n: "))
rec = 0
i = 1
while i <= n:
nota = float(input("Digite uma nota: "))
if nota >= 3.0:
if nota < 5.0:
rec = rec + 1
i = i + 1
print(rec,"alunos ficaram de recuperação")
Solução 3:
O Python ainda permite uma terceira solução,
na qual o intervalo numérico é especificado de modo mais similar
a nossa linguagem, usando operadores de comparação de forma encadeada:
n = int(input("Digite n: "))
rec = 0
i = 1
while i <= n:
nota = float(input("Digite uma nota: "))
if 3.0 <= nota < 5.0:
rec = rec + 1
i = i + 1
print(rec,"alunos ficaram de recuperação")
No entanto, essa versão não é recomendada por não possuir
um padrão equivalente em outras linguagens,
o que pode gerar erros ao transcrever a solução para outras linguagens. Um exemplo desse erro no caso da linguagem C é explicado no quadro de curiosidades abaixo.
Curiosidades:
Em linguagem C, a construção
30 <= nota < 50 para testar se a nota está no intervalo de recuperação não produz o efeito desejado. No entanto, ela não gera um erro de sintaxe e sim um erro de lógica, sendo, portanto, mais difícil de localizar e corrigir.
Por exemplo, considere o seguinte código em C.
#include <stdio.h>
int main(){
float nota;
int rec;
nota = 8.0;
rec = 3.0 <= nota < 5.0;
if(rec)
printf("Ficou de recuperação!\n");
return 0;
}
Vamos analisar o comando
rec = 3.0 <= nota < 5.0;
da sétima linha do código acima. Com exceção do ponto e vírgula presente no final do comando,
que faz parte da sintaxe da linguagem C, o resto da linha é praticamente idêntico a um código em Python.
Em linguagem C, os operadores relacionais são operadores binários, que operam sobre dois operandos e que produzem como saída 0 ou 1, representando
False ou
True, respectivamente.
Como na sétima linha do código temos
dois operadores relacionais (
<= e
<) que possuem o mesmo nível de precedência, eles são executados
da esquerda para a direita.

Portanto, primeiramente executamos o operador "Menor ou igual a" (<=), comparando 3.0 com o valor 8.0 em nota, o que produzirá 1 (verdadeiro). Esse valor resultante 1
será então comparado pelo operador < com o 5.0,
produzindo 1 (verdadeiro) como saída. Ou seja, o aluno com nota 8.0
será considerado indevidamente como estando de recuperação, segundo o código acima. Portanto, para testar intervalos em C,
precisamos necessariamente do uso do operador lógico "and" (que em C é escrito como &&).
Para o exemplo acima, a construção correta em C seria:
rec = 3.0 <= nota && nota < 5.0;
Problema 3:
Dados números inteiros n, i e j,
todos maiores do que zero, imprimir
em ordem crescente os n primeiros
naturais que são múltiplos de i ou
de j e ou de ambos. Por exemplo,
para n=6, i=2 e j=3 a saída deverá ser:
0 2 3 4 6 8
Primeira solução:
Testa os números 0, 1, 2, ... verificando
e imprimindo quais são múltiplos de i ou j,
até que n múltiplos sejam impressos.
# dados de entrada
print("Cálculo dos n primeiros múltiplos de i ou de j")
n = int(input("Digite n: "))
i = int(input("Digite i: "))
j = int(input("Digite j: "))
cont = 0 #conta quantos múltiplos foram impressos.
cm = 0 #candidato a múltiplo.
while cont < n:
if cm%i == 0 or cm%j == 0:
print(cm)
cont += 1
cm += 1
Segunda solução:
Mais elaborada. Faz menos iterações que a anterior.
A cada iteração imprime um múltiplo de i ou j.
# dados de entrada
print("Cálculo dos n primeiros múltiplos de i ou de j")
n = int(input("Digite n: "))
i = int(input("Digite i: "))
j = int(input("Digite j: "))
multi = 0 # múltiplos de i
multj = 0 # múltiplos de j
cont = 0 # conta quantos múltiplo foram impressos
while cont < n:
if multi < multj:
print(multi)
multi += i
elif multj < multi:
print(multj)
multj += j
else: # multi == multj
print(multj)
multi += i
multj += j
cont += 1









