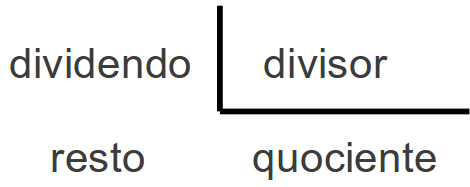
//%a,b,c e d, tal que a = 1.3432, b = 342.02,
c = 3000.8023 e d = 20900.978234,
faça um programa que exibe os 4 valores com duas casas de precisão após a vírgula, e na forma de uma tabela, conforme o
exemplo abaixo:
| a: 1.34 | b: 342.02 | | c: 3000.80 | d: 20900.98 |
Solução:
print("| a: %8.2f | b: %8.2f |"%(a,b))
print("| c: %8.2f | d: %8.2f |"%(c,d))
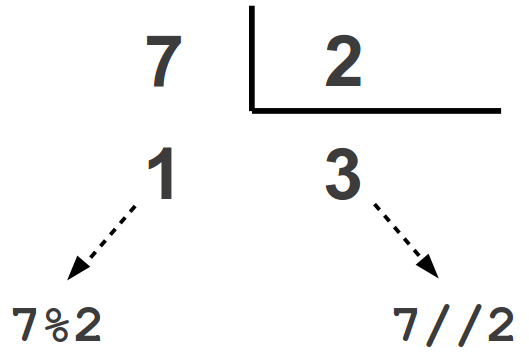
| Operador | Nome | Explicação | Exemplos |
|---|---|---|---|
| // | Divisão Inteira | Retorna a parte inteira do quociente | 7 // 2 retorna 3 |
| % | Módulo | Retorna o resto da divisão | 7 % 2 retorna 1 |
 |
 |
x é par ou ímpar,
devemos verificar se x é divisível ou não por 2.
Veja abaixo alguns exemplos de comandos digitados no prompt (>>>) do Python shell:
>>> x = 5>>> x % 2 == 0 #Testa se x é par.False>>> x % 2 == 1 #Testa se x é ímpar.True>>> x = 6>>> x % 2 == 0 #Testa se x é par.True>>> x % 2 == 1 #Testa se x é ímpar.False
O dígito menos significativo de um inteiro contido em uma
variável x pode ser obtido tomando o seu resto da divisão por 10, isto é, r = x % 10. Uma vez processado esse dígito em r, podemos então
removê-lo de x usando sua divisão inteira por 10, isto é, x = x // 10. Repetindo o processo, podemos
então acessar os demais dígitos, do menos significativo
em direção ao mais significativo.
Veja o exemplo abaixo digitado no prompt (>>>) do Python shell:
>>> x = 6583>>> x % 103>>> x = x // 10>>> x % 108>>> x = x // 10>>> x % 105>>> x = x // 10>>> x % 106
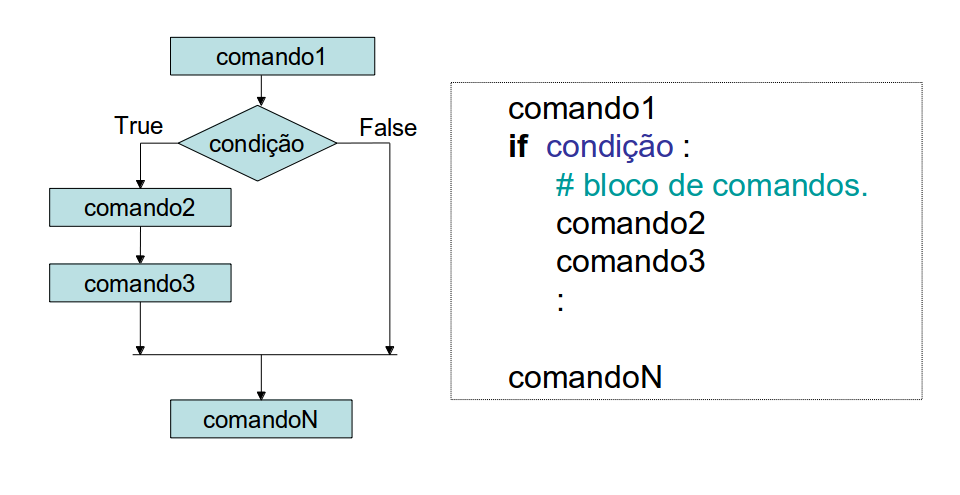
Permite a escolha de um grupo de comandos
(bloco de comandos) quando uma determinada
condição lógica é satisfeita.
6 -2 7 0 -5 8 4
o seu programa deve escrever o
número 4 para o número de pares.
Uma primeira solução é apresentada abaixo.
n = int(input("Digite o tam da seq: "))
conta_par = 0 # Contador de números pares encontrados.
i = 1
while i <= n:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: # Testa se num é par.
conta_par = conta_par + 1
i = i + 1
print("Quant. pares =", conta_par)
# Fim do programa.
Uma segunda versão que decrementa o próprio valor em n
para controlar o laço.
n = int(input("Digite o tam da seq: "))
conta_par = 0 # Contador de números pares encontrados.
while n > 0:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: # Testa se num é par.
conta_par = conta_par + 1
n = n - 1
print("Quant. pares =", conta_par)
# Fim do programa.

6 -2 7 0 -5 8 4
o seu programa deve escrever o
número 4 para o número de pares e
2 para o de ímpares.
Uma primeira solução é apresentada abaixo, usando a estrutura condicional composta.
n = int(input("Digite o tam da seq: "))
conta_par = 0 # Contador de números pares encontrados.
conta_imp = 0 # Contador de números ímpares encontrados.
while n > 0:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: #par
conta_par = conta_par + 1
else: #ímpar
conta_imp = conta_imp + 1
n = n - 1
print("Quant. pares =", conta_par)
print("Quant. ímpares =", conta_imp)
# Fim do programa.
Note que podemos evitar o comando condicional composto na resolução desse problema, dado que a quantidade de números ímpares pode ser obtida por exclusão, subtraindo-se do total o número de pares encontrados.
n = int(input("Digite o tam da seq: "))
n_salvo = n
conta_par = 0 # Contador de números pares encontrados.
while n > 0:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: #par
conta_par = conta_par + 1
n = n - 1
print("Quant. pares =", conta_par)
print("Quant. ímpares =", n_salvo - conta_par)
# Fim do programa.
Solução:
A estratégia aqui adotada é ler o número n como um inteiro e dividi-lo sucessivamente por 10 até que o resultado seja zero.
Durante o processo de divisões sucessivas, vamos nos desfazendo gradualmente dos dígitos menos significativos em direção aos mais significativos, obtendo cada um dos dígitos pelo uso do operador de resto de divisão por 10 e contabilizando o número de ocorrências do valor em d.
n = int(input("Digite o valor de n: "))
d = int(input("Digite um dígito [0,9]: "))
num = n
cont = 0
while n != 0:
r = n % 10
if r == d:
cont = cont + 1
n = n // 10
print(d,"ocorre",cont,"vezes em",num)
Solução:
#Inverte dígitos:
n = int(input("Digite o valor de n: "))
inv = 0 # variável que irá armazenar o valor de n com os dígitos invertidos.
while n != 0:
r = n % 10
n = n // 10
inv = inv * 10
inv = inv + r
print("Invertido:", inv)
Solução 1:
n = int(input("Digite o valor de n: "))
i = 1
while i*(i+1)*(i+2) < n:
i = i + 1
if i*(i+1)*(i+2) == n:
print("É triangular, ",i,"*",i+1,"*",i+2,"=",n,sep="")
else:
print("Não é triangular")
Solução 2:
Uma segunda versão mais elaborada com códigos de formatação no print.
n = int(input("Digite o valor de n: "))
i = 1
while i*(i+1)*(i+2) < n:
i = i + 1
if i*(i+1)*(i+2) == n:
print("É triangular, %d*%d*%d=%d" %(i,i+1,i+2,n))
else:
print("Não é triangular")
Exemplo: raiz de 9801 = 99 = 98 + 01.
Portanto 9801 é um dos números a ser impresso.
i = 1000
while i <= 9999:
d1 = i%100
d2 = i//100
if (d1+d2)*(d1+d2) == i:
print("Raiz de",i,"é",d1+d2)
i = i + 1