Introduction to Image Operator Learning

A large number of Image Processing and Computer Vision problems, such as Optical Character Recognition (OCR), Face Detection, Object Detection and Document Analysis, are essentially Machine Learning problems. These problems involve predicting a class either from parts of an image (in the case of OCR, regions of the images are classified as letters) or from the whole image (in Document Analysis, it may be desired to differentiate documents types). Although many different methods exists to solve these problems, most of the algorithms are developed exploring characteristics implicit to their domains of application. Also, these algorithms require deep knowledge of both Image Processing/Computer Vision and the domain of application, making them hard to approach by non-experts. Image Operator Learning proposes an alternative approach. Instead of treating each problem individually, we use the following generic formulation based on Machine Learning.

Given pairs of images containing an input image I_i and its processed form O_i, estimate the transformation f(I_i) = O_i with minimum error. The estimation must also have small error in images belonging to the same domain as I_i. The transformation f is called an Image Operator.

Image Operator Learning studies how to estimate the transformation f . In particular, W-Operator Learning, which is the focus of TRIOS, represents f as a local transformation. To determine the value of pixel p in the output, only a fixed neighborhood W around p is analysed. The local transformation f : 𝒫 (W) → 𝓛 is called W-Operator and its neighborhood W is a Window. 𝓛 is the range of values present in the output images.

W-Operator Learning

The estimation process of W-Operators is divided in three main steps. In the first step, Feature Extraction, we calculate the joint frequency for all the patterns that occur in the input images and their respective outputs. In the second step, Optimization, we minimize the error in the training images by assigning the optimum label for all the observed patterns. The third step, Generalization, uses a classifier to assign labels to the unobserved patterns. This process was first presented in papers [1] and [2] by Edward Dougherty.

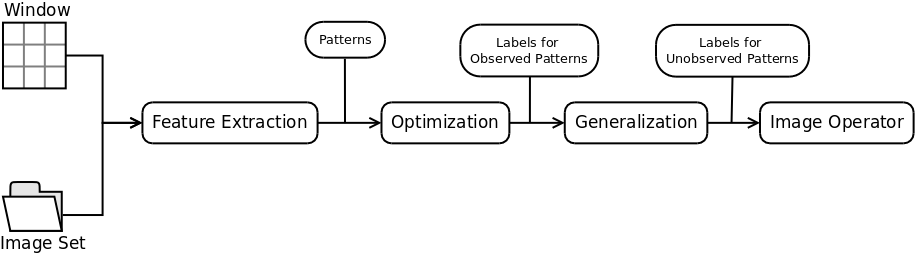
Figure 1. Training process for Image Operator Learning.

Suppose that the {I_i} and {O_i} sequences of images come from jointly stationary processes (I, O) . Let W be a finite Window. The Mean Square Error of the W-Operator f_W defined by a Window W with respect to (I, O) is

where I_-z denotes the translation of I by z. w_z = I_-z ∩ W contains all pixels around z that belong to the Window W. w_z is a window configuration and, together with O(z) , comprehend all the information that will be analysed by the training process. The extraction of the pairs (w_z, O(z)) for all pixels z in all pairs (I_i, O_i) is done at the Feature Extraction step.

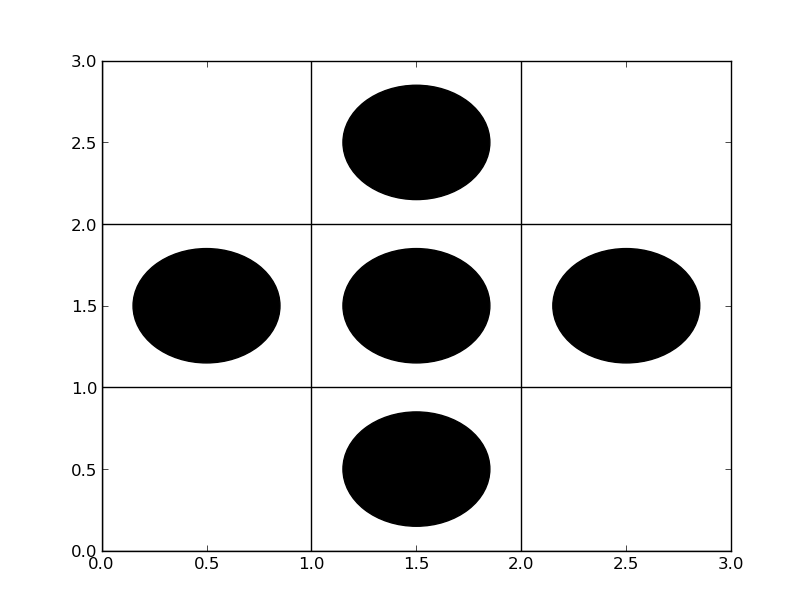(a) Cross shaped Window.	(b) Window positioned on a pixel.	(c) Window configuration extracted.

Let X_z = I_-z ∩ W , then X_z is a random vector. Let Y_z = O(z) be a random variable that holds the value of O in the pixel z. Since I and O are stationary, z may be dropped and (X, Y) characterizes (I, O) locally with respect to W . Therefore,

The optimal MSE estimator is E[Y|X] . In other words, an Image Operator F is optimum with respect to the MSE if F(x) = ∑_y y P(x, y) . In practice, the distribution P(X, Y) is unknown, but can be estimated using the frequency of the pairs (w_z,O(z)). The assignment of the labels that minimize the MSE is done in the Optimization step.

Finally, it is possible that some relevant patterns do not appear in the input images. The Generalization feeds a classifier with the data provided by the Optimization step to obtain labels for the unobserved patterns. It is important that the classifier does not change the decision for the observed patterns.

Algorithm for W-operator learning

TRIOS implements the following algorithm for W-Operator learning.

1. for each image pair (i, o) in the training set do:
2.     for each pixel z in i do:
3.         w_z = I_-z ∩ W
4.         freq[(w_z, o_z)] += 1
5. for each observed pattern w_z do:
6.     label[w_z] = ∑_y y (freq[(w_z, y)]/freq[w_z])
7. train a classifier using the pairs (w_z, label[w_z]). It is necessary to mantain the labels assigned in the previous step.

The Incremental Splitting of Intervals (ISI) algorithm (described in [3]) produces binary W-Operators with good performance. Decision Trees are used for Gray-level Operators.

The application of the Image Operator follows the same steps. First the patterns w_z are extracted positioning the window W at each pixel z. Then the value of pixel z in the output is the result of the classification of the pattern w_z.

Challenges and Open Problems

W-Operator Learning for Gray Level images is still a challenge due the size of the space of possibilities. There are k^|W|k possible local transformations, where |W| is the size of the window and k is the range of gray level of the images. In this case the Generalization error is very high, since most of the relevant patterns are not observed. Aperture Operators [4] try to mitigate this effect by restricting the range of gray levels considered. However, it is still necessary to determine an adequate range of gray levels and an adequate Window.

As seen previously, the Window W used in the Feature Extraction step determines the probability distribution P(X, Y). If W is too small, the resulting W-Operator will fail to discriminate larger patterns. If W is too large, too many relevant patterns will not be observed, lowering the quality of the estimation of P(X, Y) and increasing Generalization error. The Window Selection is a Feature Selection problem and is one of the open problems in W-Operator learning.

Finally, Multi-Level Operator training[5] improves the W-Operator training presented previously by combining the results of many Image Operators designed with different windows. The result is a W-Operator that effectively uses a large window but does not have a large Generalization error. It is necessary, however, to determine 1. the number of operators combined and 2. the window of each individual Image Operator.

Bibliography